On the Topic of Changing the Card Drop Formula

[The G-Meister]

This post is far too long for the forums, so I've split it up into 2 extra replies. Unfortunately the forum play havoc with the display of equations, so anything in square brackets at the end of an equation is the equation number.

Contents

1. The Introduction
....1.1. A Quick Disclaimer
....1.2. Reader's Guidance
2. The Current System (Geometric Distributions)
....2.1. The Context
....2.2. The Maths
........2.2.1. How Probability of Card Drop Varies with Number of Kills
........2.2.2. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills
........2.2.3. The Aftermath
....2.3. The Graphs
3. The Other End of the Scale (The Unit Step)
....3.1. The Maths
........3.1.1. How Probability of Card Drop Varies with Number of Kills
........3.1.2. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills
....3.2. The Graphs
4. And Everything in Between (Weighted Geometric Distribution)
....4.1. The Introduction
....4.2. The Maths and Graphs
........4.2.1. How Probability of Card Drop Varies with Number of Kills
........4.2.2. Approximation to Unit Step
........4.2.3. Approximation to Geometric
........4.2.4. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills
........4.2.5. The Scaling Factor
........4.2.6. The Remaining Graphs
....4.3. The Context
....4.4. The Implementation
5. How to Argue About This Topic
....5.1. I prefer the way the game currently works
....5.2. I would prefer the unit step
....5.3. I would prefer minimal weighting
....5.4. I would prefer a little weighting
....5.5. I would prefer moderate weighting
....5.6. I would prefer significant weighting
....5.7. My name is Own and 1% should be added to the drop rate after 1000 kills
6. A Note to the Developers
7. The Software Tool
8. The Epilogue

1. The Introduction

I hope no-one reading this is vegetarian or vegan, as you're going to be insulted at how meaty this article is. Jokes aside, actually take a look at the scroll bar, and actually go and grab a meal, because you'll probably need one at some point while reading. Despite the length, I would still advise reading the whole article, no matter what your level of experience in mathematics. While I tell certain people to dip out at certain sections, I use similar processes throughout, so understanding the ones at the start will give context to the ones elsewhere.

1.1. A Quick Disclaimer

If you've come here to express your views on what kind of solution you would like to see, I have just the section for you! Having said that, while you could quite easily scroll down to section 5, pick a group and go, without context it's a little fruitless. I'd still recommend reading the whole article, though if you can read and make sense of the graphs and equations, you should be set.

1.2. Reader's Guidance.

Our process here is gonna go like so. First, we'll explain how the game currently drops cards in words. We'll then translate that into simple maths, with some helpful graphs. We'll then move onto how this maths can be adapted to change how the RNG works, briefly dipping in to some higher-level maths, but providing yet more graphs and pictures for the layman. Finally, we round off by translating it back into words.

And the last thing before we move onto serious stuff, I believe there is limit of 10 files that can be uploaded to a single post. I assumed I would go well over that, and as such many of the images have been compacted together into single, larger images. Don't worry though, I make sure to reference them all throughout the text and in the right order.

2. The Current System (Geometric Distributions)

A lot of the information in this section can be found on the equivalent Wikipedia page, but here I have tried my best to put it both in normal people's words and in context, in the interest of readability.

2.1. The Context

Card drops in the game currently follow a geometric distribution. Keep that word in your head, we're gonna be using it a lot. For a geometric distribution to be obeyed, there are 3 criteria. Firstly, all trials (instances where a single, random "test" is carried out) must be independent and affect each other in no way. Secondly, there can only be two possible outcomes of these trials, often designated a success or failure. Thirdly, the probability of this success must be constant. If all three of these are true, the geometric distribution shows how likely it is to get the first success on any given trial.

This might sound like total jargon to anyone not vaguely familiar with statistics, but actually it's very easy to translate into the game's card drop mechanics. Each "trial" is a "kill", the "success" is the drop of a card, and cards only drop once, meaning we only consider the first "success". With that in mind, the three criteria are obeyed. The outcome of one kill (being card drop or no card drop) does not affect the outcome of any other, cards can either drop or not drop, and there is mountains of evidence that the probability of a card drop is constant.

2.2. The Maths

I tried my best to explain the graphs without the maths. Unfortunately I could not, so you'll get them later There are lots of letters from this point onwards, and I’m not just speaking about the multiple thousand words of explanation. All variables being used as part of the maths should be in italics. If you spot one that isn’t, or a sentence that reads weird, pop a reply down.

The letter we will be using for "number of kills" is x. This is because all of the graphs will have the number of kills on the x-axis (along the bottom). We'll use p for the fixed drop chance.

2.2.1. How Probability of Card Drop Varies with Number of Kills

Simple answer, it doesn't, exactly as we just said in section 2.1. above. You might be asking what the point of this section is. It is less that I want to explain how this works, but more that I want to include it for completeness before we change the maths in it later. Having said that, it does have an important consequence. If the probability of success is constant and we can only have a success or failure, by logical deduction, the probability of failure must also be constant. Assuming all probabilities add up to 1 (which is a general assumption used throughout all of the mathematical topic), that probability is 1 - p. We will be using this in a moment.

2.2.2. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills

This is where the distribution part comes in. While the drop chance of a card is constant, the amount of kills you have to make to get it behaves a little differently. Let's take an average sample of people (and by that I mean they behave exactly as theory predicts) and run them through the card drop process.

Here is where mathematical statements start. I'm going to write down an equation and explain what it means in words underneath.

P(X = 1) = p [1]

This might look very confusing for a few of you. What it says is "The probability of people getting a card drop on the first kill is equal to probability of a card drop". That should be a lot easier to understand, and fairly self-explanatory from what we have explained already (as well as a "no shit sherlock" statement). Basically, the number after "X =" is the number of kills, and everything after the second equals sign is the probability. Everything else is mathematical terminology you can safely ignore. Onto our next kill.

P(X = 2) = (1 - p) * p [2]

This translates to "The probability of people getting a card drop on the second kill is equal to the probability of failing to get a card on the first kill, multiplied by the probability of a card drop". That should be a reasonable deduction when people can only get one card. The people who got a card on the first kill we don't want to be considering any more, as they would never reach this point in the distribution. If you've wrapped your head around that, we follow a similar process for the third kill.

P(X = 3) = (1 - p) * (1 - p) * p = (1 - p)^2 * p [3]

This translates to "The probability of people getting a card drop on the third kill is equal to the probability of failing to get a card on the first and second kill, multiplied by the probability of a card drop". If you understood the process for the second kill, we have only done the same thing here for the third. The only extra thing we have done is re-write the probability of failing to get a drop for all of the previous kills. This is nice simplification for the step below.

Here, you should have an idea of the process. The last thing to do is extrapolate said process over all kills.

P(X = x) = (1 - p)^(x - 1) * p [4]

This reads "The probability of people getting a card drop on the xth kill is equal to the probability of failing to get a card to the power of (number of kills - 1), multiplied by the probability of a card drop". If that seems like a bit of a jump, run it though backwards, like so.

P(X = 3) = (1 - p)^(3 - 1) * p = (1 - p)^2 * p [5]
P(X = 2) = (1 - p)^(2 - 1) * p = (1 - p)^1 * p = (1 - p) * p [6]
P(X = 1) = (1 - p)^(1 - 1) * p = (1 - p)^0 * p = 1 * p = p [7]

If those look confusing, we are replacing our variable x, the number of kills, with a specified number we'd actually like to find the probability for. Anything to the power of 1 is itself, used in Equation 6, and anything to the power 0 is 1, used in Equation 7.

2.2.3. The Aftermath

Pun intended. The equation we are left with, describing the geometric distribution as a whole, is Equation 4 above. This has some interesting properties. Firstly, by taking a weighted average of this distribution (check this Wikipedia page or Google it for more info) we find that the average person gets a card drop at 1 / p kills. To make things a little clearer, if the drop chance is 1 / 300, then the average person gets a card drop at 300 kills. We will be using this property later. Secondly, the only letters on the right hand side are p and x. As x is a variable we change to get distribution frequencies, p is the only parameter of the distribution. By parameter, we mean a variable that is defined when the distribution is made.

Together, these two things demonstrate an underlying property that defines a geometric distribution - the fact that it is completely random. The distribution and all of the properties associated with it depend only on the fixed drop chance p, and at no point is a card drop ever guaranteed. This means it is possible (though impossibly unlikely) that You reach up into the 10s of thousands of kills, completely empty handed.

The actual property that defines complete randomness is the card drop probability never reaching 1, or being certain, at any point. However in this case, the geometric is by far the simplest of these types of distribution.

2.3. The Graphs

To round off the geometric distribution, let's give some graphs of its function. These basically put all the maths we did above into pictures. All graphs are using the same drop chance, simply displaying the data in different ways.



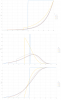
The first graph is one of the card drop probability against number of kills, explained in 2.2.1. As you can see, it is constant for all kills, as we have said already many times. For now this is just for completion, as we will be including similar graphs later.

The second graph is one of Equation 4 that we derived in 2.2.2., that being the probability of reaching a given number of kills for a first card drop, plotted against the number of kills. We have P(X = x) on the y-axis, and x on the x-axis (see, calling the number of kills x did come in useful!). If you are confused as to why this decreases with the number of kills, look at the two parts of Equation 4. We have a constant p, multiplied by a "failure factor" of (1 - p)^(x - 1). This "failure factor" takes all the people that did not get a card drop on previous kills, and is what is actually decreasing. As 1 - p will always be between 1 and 0, raising it to a positive power will always cause the number to decrease. If you're still confused, just ignore it and take a look at the explanation of the third graph below, it's not the end of the world.

The third graph hasn't been explained anywhere yet, but it should be simple to understand. All we have done is taken the probability for each kill on the second graph and added it to that of all the previous kills. Mathematically, this gives us a sum of all the successes up the that point, known as a "cumulative distribution". In context, this is everyone who has got a card up to that point. This increases with the number of kills, just as you'd expect. This should be easier to digest in general as well as being a graph that fits nicely with multiple lines, so I generally refer to this one. For now, we're done with the geometric distribution (finally!).

3. The Other End of the Scale (The Unit Step)

Before we get on to the distribution I have been designing, I'd like to pop a quick word in about the exact opposite of the geometric distribution. The opposite of something that is completely random is something that is completely certain. This means that there is no factor influenced by randomness included in any of the calculations. Instead of having a fixed drop chance, we instead have a fixed number of kills at which a drop is guaranteed, and impossible beforehand. Let's make this a variable, and call it m. Using this, we can follow the process we did for the geometric distribution. The thing we end up with is a function called a "unit step", where the graph hops from 0 (no chance of drop) to 1 (guaranteed drop) instantaneously. As soon as we have a 1, the rest of the distribution is irrelevant, as everyone will have their card.

3.1. The Maths

3.1.1. How Probability of Card Drop Varies with Number of Kills

In maths, this gives us two statements.

p(x) = 0 (1 ≤ x < m) [8]
p(x) = 1 (x = m) [9]

On the left of the first equals sign, the p(x) means the probability of a card drop as a function of x. In the equivalent section for the geometric distribution, 2.2.1., I didn't give this notation to avoid extra confusion, as it would've read "p(x) = p". Equation 8 states that "the probability of a card drop on the 1st to (m - 1)th kill is 0". Equation 9 states that "the probability of a card drop on the mth kill is 1".

3.1.2. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills

The fantastic thing about the unit step is, when we consider how many kills people get their card drop at, it follows exactly the same pattern as in 3.1.1. above.

P(X = x) = 0 (1 ≤ x < m) [10]
P(X = x) = 1 (x = m) [11]

If the 1 in Equation 11 seems confusing, all it means is that 100% of people get their drop when the number of kills equals m, exactly as we intended.

3.2. The Graphs

And the helpful graphs return once again.



The first graph shows the probability of a card drop against the number of kills. Hey look, it's 1, or 100%, at the value of m we are using. The second graph shows how many kills people make for a card drop against the number of kills. Hey look, it's 100% at the value of m we are using. The third graph shows the sum of how many people have a card drop against the number of kills. Hey look, it's 100% at the value of m we are using.

You get the idea.

4. And Everything in Between (Weighted Geometric Distribution)

4.1. The Introduction

We have two ends of a scale now. We have complete randomness, and complete certainty. To fill in the gap between them, we need a system that has a bit of both of these factors. The question is, how do we make one?

The way we go about weighting a distribution, be it between random and certain or otherwise, is by changing the graph of the probability of a card drop. You do this by making the probability a function of the number of kills. This is true for all distributions that aren't the geometric distribution, including the unit step. If you want to be nicer to players than the geometric distribution is, you increase that probability with the number of kills. However, this is where we open up completely and can put almost any graph in. Instead of explaining what we should want out of this graph, I am instead going to propose the solution I have been designing and talk about its consequences afterwards.

Clean your ears out MLG.

 

[The G-Meister]

4.2. The Maths and Graphs

4.2.1. How Probability of Card Drop Varies with Number of Kills

The equation which I have been working with for a weighted probability of a card drop looks like this.

p(x) = e^(a * (x - m)) [12]

Here is my proposition for a weighted geometric (or simply just weighted) distribution, with more unfamiliar letters. Thankfully, I've shown some of these already, and they have the exact same use. x is the number of kills. m is similar to the m used in the unit step, and is the number of kills at which a card drop is guaranteed (meaning the probability is 1). e is new for this article, and is a defined constant with a value of roughly 2.72, known as Euler's number (it has important properties I'm not going to explain here). Finally, a is the most unique of the lot, being an unknown "scaling factor", which we have to calculate, based on one more parameter which isn't in the equation. This parameter we will refer to as k, and is equal to the intended mean of the distribution (the average number of kills at which someone gets a card drop).

To take the edge off of all this complexity, let's throw you a graph straight away.



Now this graph has a lot to explain. This graph is a plot of the probability of a card drop against the number of kills, using Equation 12. The different lines have different values of m. k in this case is set to 50, which is simply a value I use for testing. 50 gives enough data to get the essence of the distribution, but not so much as to make Excel explode (we'll save that part for later ). The key on the right shows which colour line has which value of m. The value of a, while irrelevant for this section, does change with each line, as its value depends on both k and m.

Some of you may have spotted something familiar about some of these lines. If you haven't yet, the m = 50 line is vertical, just like the unit step distribution, and the m = 10000 line is horizontal, just like the geometric distribution. We will cover how this works in a second. For now, these graphs have some properties I would like to examine. Firstly, they all reach 1, a guaranteed card drop probability, at their value of m, just as we intended. Secondly, the three middle graphs have a visible curve to them. This curve is typical of an exponential, having a flat-ish region near the start, moving towards a steeper curve near the end.

This shows the approach I have gone for is to increase the drop with each kill multiplicatively. Each point on this line is a multiple of the previous, no matter how small that multiple might be. Let’s move on to some of the fantastic consequences this has.

4.2.2. Approximation to Unit Step

Here is an explanation of how we can get the weighted distribution to act like the unit step. As we have already shown in 3.1.1., the unit step can be used like a probability distribution when the probability of a card drop is 1 at the intended mean and 0 otherwise. The way this is done with the weighted distribution is by making m = k. This means Equation 12 becomes

p(x) = e^(a * (x - k)) [13]

However, what happens to the scaling factor a in this scenario? Running it through calculation, we find that a becomes what is known in physics as "large". This is an approximation where a number is large enough to act like infinity. Now don’t worry if you don’t quite understand the concept behind infinity, all you need to know is it’s very big. Either very negatively big, or very positively big. And yes, you can use it in maths, like we are about to.

In physics, we occasionally like to straight up swap in the values we approximate, much to the offence of any mathematicians. Thankfully, not only is this a very minor sub-section, but also, in game development, similar approximations can be made without having a significant impact on gameplay. Regardless, here are the effects this has on Equation 13.

p(x) = e^(∞ * (x - k)) [14]

Now, in the exponent (the part in brackets), the infinity term completely dwarfs the (x - k) term. However, the (x - k) term undergoes what's called a "sign change" at x = k. What this means is it changes from negative to positive, making the infinity term also go from negative to positive. This means we can make some simplifications.

p(x) = e^(-∞) = 0 (x < k) [15]
p(x) = e^(+∞) = ∞ (x > k) [16]

If you haven’t seen exponentials before, this might be a bit confusing. Go for a google if you want to know more, but this is a useful property of exponentials.

That's most of the approximation out the way. Before k, we have zero probability for a drop. After k, we have infinite probability for a drop. This seems a little overkill, but frankly it works exactly the same as having a 100% drop chance, as you can only get one success per trial. However, we're missing out one crucial thing here, which is what happens at x = k (which also equals m, remember).

What actually happens is we get 0 * ∞. This is a complicated mathematical conundrum which is currently beyond my knowledge. However, we can avoid this problem entirely because a is not actually infinity. It will always be in a finite range, and the joy of approximations is that you can pick and choose the properties of them depending on relevancy. For those of you interested on the problem, Google is your friend. For us, we are going to do this instead.

p(x) = e^(a * (k - k)) = e^(a * 0) = e^0 = 1 (x = k) [17]

And there's our one, just as it was originally. Thankfully the rest of the distribution is irrelevant after k, and as such we never reach the infinities.

4.2.3. Approximation to Geometric

We're going to take an easier approach with this approximation. I don't quite know how to follow the maths all the way through, but we have already seen the approximation in action in Graph 4.2.1. A. As such, we'll be a little less rigorous and a little more offensive to the mathematicians.

This time, m instead of a becomes "large". This has different effects on Equation 12. If you look back at it, there is the (x - m) term in the exponent (the part in brackets). When m is large, it will completely dwarf the x part. This is because a small change in x has very little effect on the overall (x - m) term. Consequently, the (x - m) approximates simply to (- m) for small x. This means Equation 12 becomes

p(x) = e^(a * (- m)) = e^(- a * m) (small x) [18]

This means we are left with an equation involving only constants, just like the geometric, except this time the format is a bit weird. However, once again, we are left with the scaling factor question. This is the part I do not have the mathematical ability to solve. However, we have already shown the equation making a working line in Graph 4.2.1. A, so it should be possible to work it backwards from that with the help of calculated values. I won't follow this through as I believe we have said and shown enough already.

4.2.4. How Probability of Reaching a Particular Number of Kills for a Card Drop Varies with Number of Kills

This is the section that anyone not particularly familiar with the topic of probability can probably skip. Scroll down until 4.2.5. We're only going to follow the same process we went through in 2.2.2., by simulating a group of people through the probabilities, just this time with different probabilities. After that, I'd like to ask for some help from anyone more versed in maths than I am.

This is where we start back on the equations again. As I'm assuming the less familiar people have already skipped on, I'm going to take less time to explain the basics and get into the specifics and differences from the process in 2.2.2. Here's our first equation.

P(X = 1) = e^(a * (1 - m)) [19]

The probability of reaching one kill for a card drop. It only gets worse from here on out.

P(X = 2) = (1 - e^(a * (1 - m))) * e^(a * (2 - m)) [20]

The probability of reaching two kills for a card drop. Just like in 2.2.2. we are multiplying the probability of failure to get a drop on the first kill (the first term) by the probability of success on the second (the second term). You might see where this is going.

P(X = 3) = (1 - e^(a * (1 - m))) * (1 - e^(a * (2 - m))) * e^(a * (3 - m)) [21]

The probability of reaching three kills for a card drop. If you didn't see this coming, this is an unfortunate consequence of weighting. As soon as the probability of a card drop involves x, the simplification of (1 - p)^(x - 1) used in 2.2.2. no longer works, as 1 - p is no longer constant. This means we end up with an ever-expanding formula unless we use some fancy mathematical notation. Thankfully, at least it exists, and I'll use it.

[22]

And there's your equation for any number of kills. The capital pi notation here is denoting the multiplication of the series. Here, it caps at x - 1, meaning the larger the number of kills you're trying to calculate, the more terms you have to multiply by. This makes it very difficult for a sane human to get a number out of, and that is why I employed the help of computers - again, a later topic.

I also think this equation is slightly wrong, as when x = 1, the multiplicative series runs from i = 1 to 0, and I have no idea how that works. Basically, the whole series should be 1 in that case. Assume this for every time something similar pops up, whether it be the section below, or the talk about the computer tool in the appendices.

4.2.5. The Scaling Factor

Welcome back everyone, time to get back to readable and sensible maths in the realm of normality and not utter confusion (I hope)!

Now is the point where we have enough maths to explain how this scaling factor is defined. We need to take the already messy equation we made above and take the weighted average of it, just like we did in 2.2.3. for the geometric. This weighted average is defined as being k, the intended mean (different ways of saying the same thing). And as such, we have the definition of a.

[23]

Now it's even more complicated. This is even worse to calculate by hand, as you might be able to imagine. To everyone confused at the sight of this unholy abomination, don't worry about trying to understand it. All you need to know is the important fact that there is no sane way that I know of to get the scaling factor in one easy formula. As such, I have built a piece of software that calculates this value by trial and error, and for our purposes here, this method is more than accurate enough for what we need. I'll get back to the software later.

However, this is where I'd like to ask for help from anyone capable. Any other method of calculating the scaling factor would be more useful here. If you can get this formula into an iterative state, find a good way to approximate by integration, or even just simplify the darn thing, I'd be incredibly grateful. Feel free to pop any ideas or completed work in this thread, or by PMming me either here or on Discord.

4.2.6. The Remaining Graphs

The other two graphs to complete the usual set of three are present below, along with their explanations.



Before I explain these graphs, I want to point out a small change they have. In the key, I have added the corresponding multiples of k for each value of m. Nothing has really changed, as the value of k is still 50 for all lines. However, what is more important is the fact that, instead of using m as a fixed number irrespective of k, we can do this, allowing us to change k, resulting in very similar graphs. This gives another option when it comes to implementation, which we will cover in a bit.

The first graph shown here is that of Equation 16, being the probability of reaching a certain number of kills, plotted against the number of kills. Again, one line follows the same path as the geometric, and another follows that of the unit step. For readability I've actually scaled the y-axis down here, as otherwise the unit step would dwarf all the other lines. We know how the unit step works and it's pretty obvious where it's going. In regards to the other three lines, they go all over the place. One has a peak to the right of the mean, another spreads out a little and the last has a more gradual descent. The reason for all these weird shapes is the fact that you have an exponentially increasing probability vs. an exponentially decreasing number of players. There can be balance between these two, or one completely dwarfing the other. Regardless, onto the more important graph.

The second graph is, once again, the cumulative distribution. Here's where the magic starts to look sensible. We have the line of the approximation to the geometric, and the line of the approximation to the unit step. However, the lines in between those give use a gradual shift between the two. Ta-daah! Furthermore, there is a whole spectrum of graphs not included between the approximation to unit step and the approximation to geometric, all with their own values of m.

The best way to read this graph is to look at the point at which each line pretty much reaches 1. At that point it is incredibly unlikely for anyone to get that unlucky. A lot of them do it well before their value of m, but all of them do it before the geometric does.

4.3. The Context

So what does all of this mean when we put it back in context? Originally, in the geometric distribution, we had only a single parameter defining the entire distribution, being our fixed drop probability p. In the weighted distribution, we have two, being the intended mean k, and the kill number at which a drop is guaranteed m. Funnily enough, we also said earlier that the mean of the geometric distribution is equal to 1 / p. This means that we can build the card drop system the game currently uses into this new weighted distribution, by setting k to 1 / p, and as we have demonstrated already, making m "large".

The beauty then comes in the form of being able to change the value of m. The average person will still get a drop at the same point, but it is possible to shift unlucky people from the end of the distribution back, at the expense of a few luckier people being pushed forwards (this is an unavoidable side effect if we keep the average number of kills for a drop the same).

4.4. The Implementation

Now we have all this info, how would one go about implementing it? Thankfully, this is incredibly simple. The joy of having only a single formula for the probability of a card drop (rather than a more complicated hopping between different distributions) is that you simply swap out the constant p for the formula. The only extra thing that needs to be added is a kill counter, but this would be added for any distribution other than the geometric.

I am going to make the assumption that the game currently runs the "trials" for card drops by running a test when each kill is made. This test generates a random decimal number between 0 and 1, and compares it against the fixed card drop probability p. If the random value is less than p, a card is dropped. To change this into the weighted distribution, all that is needed is a few steps.

1 - Open the software tool I have coded.
2 - Write down the value(s) of k (and m) you intend to use somewhere, as k is not stored in the code.
3 - Type "sf k m", where k is the intended mean, also equalling 1 / p of the equivalent geometric distribution, and m is the number of kills at which a card drop is guaranteed.
4 - Open the log.txt file in the folder, and copy your generated scaling factor, a.
5 - In the code, simply replace p with the code equivalent of Equation 12, e^(a * (x - m)).

Now for what this might look like in code. Originally, we might have something like

onKill()
{
    if (randomDecimal() < 0.01)
        dropCard();
 
    ...other kill things like drops and whatnot
}

where 0.01 is the fixed drop chance p, which would change to something like

onKill()
{
    incrementKillCounter();
 
    if (randomDecimal() < exponential(0.0110392568938781 * (numberOfKills() - 500)))
        dropCard();
 
    ...other kill things like drops and whatnot
}

where a = 0.0110392568938781 and m = 500. This of course would be different for each class of enemy.

Whew, I think we're finally over this section. Grats for making it this far! There isn't too much left now, only a section about how to guide your arguments, a quick note to the devs, and finally the tool, along with a download. Onwards!

 

[The G-Meister]

5. How to Argue About This Topic

Now onto the important part. With all this information, what can/can we not have a good debate about? What I'm going to do is group arguments together under similar categories so like-minded people can co-ordinate themselves within all this confusion. With that in mind, I'd suggest stating which group(s) you are backing when you make an argument, as a matter of clarity. And yes, you can be part of multiple groups depending how general you want to be.

In some of these sections I'm going to refer to setting the value of m to different multiples of k. This is because I am assuming that card drops in the game currently have their fixed drop probabilities such that enemies you kill less often while grinding have a greater drop chance, with the intent that, overall, the average person gets cards for all enemies in an area at roughly the same time. If that is the case, using m in terms of k is a lot more useful to us, as it brings the weighted distribution's fixed drop probabilities also into the same region as each other. Not only does this make for better consistency but it also means there is a fixed upper limit to the amount of time spent grinding per area.

You are more than welcome to express other opinions like preferences for other weighting styles and constant values of m for all enemies, but I don't think they will be as productive discussion or as useful as any of these.

Anyway, onto the groups. If you'd like some reference as to what changes these lines bring about, look back at graph 4.2.6. A and compare the ranges of the lines for the specified values of k.

5.1. I prefer the way the game currently works

'Nuff said really. As a matter of efficiency, it's not worth swapping to the weighted distribution's approximation to the current system when it's already implemented and working.

5.2. I would prefer the unit step

I'm assuming this will be unpopular, but it is a possibility nonetheless. If the unit step were to be implemented, we have a similar situation to above, where implementing a kill counter and giving a card drop when it hits a certain value would be much easier than implementing the weighted distribution's approximation.

5.3. I would prefer minimal weighting

This implementation would be enough for a change, but probably not so much as to deter any and all complaints about cards being bugged. I'm classing minimal weighting as implementing the weighted distribution for values of m being between 20 * k and 50 * k.

5.4. I would prefer a little weighting

By setting m between 8 * k and 20 * k, there should be a minor change in luck for everyone, and a moderate change for unlucky people, to the extent that it is likely to deter complaints from the forums entirely. And yes, that's about the best judgement I have here without diving into stats.

5.5. I would prefer moderate weighting

A value of m between 4 * k and 8 * k will give a moderate change in luck for everyone, and a significant increase in luck for unlucky people.

5.6. I would prefer significant weighting

Getting into the low bounds, a value of m between 2 * k and 4 * k will give significant change in luck for everyone. People are much less likely to see card drops early on than before.

5.7. My name is Own and 1% should be added to the drop rate after 1000 kills

A little joke from the forums. We love you really Own <3

There, that's all your groups! Now FIGHT!

6. A Note to the Developers

Now we're in the cleaning up stage, I'd like to notify the devs of something quickly, and that thing is that I would be grateful if I could know if you implement the weighted distribution. The reason for that is it is completely dependant on the tool I have coded. As such, if I make any modifications to it, I would make them as a matter of priority rather than a matter of preference. (I'd also put it on my CV but that's besides the point ).

7. The Software Tool

Hey, finally onto the software tool! I wanted to keep this section as close to the download as reasonably achievable, so it's a little far down the bottom. This tool has been used extensively in this article and was very useful throughout the process. It can do three main things. It can generate the scaling factor for weighted distributions, as we have said already. It can also generate distributions, either geometrically or weighted(ly?). By that, I mean the data in most of the graphs has been generated using this tool. It can generate these distributions theoretically, using the theory we have discussed in this article. However, it can also generate random distributions in the exact ways I have described in section 4.4., as in, the way I am assuming the game does, or will in the future.

Here's your setup instructions.

1 - You'll need Java installed. The program was built in and runs fine on Java 8, but it may work on other versions.
2 - Download the file at the bottom of this post, called "SoG Card Distribution Generator v3.0 clearlog and Release Update.zip".
3 - Put it in a destination of your choice, right click on it and select Extract All.
4 - Finally, double click on "run.bat". If a command prompt opens without any error messages then I've given good instructions and your system is intact!
5 - To get started, type "help" for a list of commands. The program should take it from there!

In your extracted folder, there is also a text file named "log.txt". The majority of the output to the console is also outputted to this text file, and makes for easy copying if your command prompt doesn't allow you to. Just be sure to re-open it each time you run a command. If it's getting too full, type "clearlog" in the command prompt to wipe it.

Other than that, there is a compiled "CardTest.jar", which "run.bat" simply runs, and the source code, in the form of "CardTest.java". The source code is present for those of you that wish to verify it is working properly, and the relevant sections have been extensively commented (denoted by // followed by text in Java). Everything else simply gets the program to work like a command prompt. Open it in a text editor of your choice, though one with uniform character spacing and Java-specific highlighting will be of great use. Finally, all of this has been copy-pasted into the README.txt in the folder.

If you would actually like to set up graphs like the ones I have here, copy-paste your numbers into Excel. Next, go to Insert > Charts, and select the one with the dots. Then select "Scatter with smooth lines". This is the graph I have been using throughout, and while I should have technically been using histograms, they are less clear to the average person and I also couldn't find a clean way to represent multiple lines on. However, they get the point across, which is what matters. You are more than welcome to use any other software for data analysis.

If you find any errors or have questions, feel free to ask me here or on Discord. If the program crashes without you typing "exit", ending in the words "Press any button to continue...", be sure to gimme a copy-paste of the text or a screenshot of the error.

A quick note - I've just realised I forgot to comment the generation of the scaling factor in the source code. I'll do that when I get back from my brief holiday to the Isle of Wight. Feel free to enquire in the mean time.

8. The Epilogue

God this was draining. Never again, please. Maths was a mistake.

~G

P.S. Have the graphs too. Extract "SoG Distribution Graphs.zip". They're in there, data and all.

 

[Teddy]

Impressive write-up, and an entertaining read, as well! I for one do not know much about statistics so some of it went over my head but most was properly educational.

I think I have Java installed already on my work computer at the office, so I'll check out the tool itself there tomorrow.

Regardless if I end up using the output of your tool, you've at the very least given me a pretty big push in the right direction towards a fail-safe for cataclysmically unlucky people! I might hack it a bit so it fits into the current system (that is, not requiring me to go through all the enemies and change values), but even so it will likely be very inspired by your article so I think you should count that as a win either way.

I'll give an update on it when I get around to do the drop chance tweaks!

 

[The G-Meister]

Sounds good man, glad you found it helpful! If there's something you feel like you needed to understand but didn't, please do say - that goes for anyone reading this too. I tried to get someone to read it through before posting so I could see if I did a terrible job, but unfortunately they got a little distracted (I'm watching you @Chaldo ):< ).

In terms of hacks I'm sure it'd be more than possible to write a method that does it. I don't know how it works in C# (or whatever language the game is written in), but a Java equivalent might be something like

public boolean getDrop(double scalingFactor, int max, int kills)
{
    return Math.random() < Math.exp(scalingFactor * (kills - max));
}

to get a true/false of card drop, or even have scalingFactor and max defined as constants for the whole class, simply parsing in the kill count on each kill. That never passed my mind really

 

[XxX_MLG Noob_XxX]

This is legitimately bothering me because so many rules are being broken. Things like the lognormal distribution are bad enough since they're piecewise. The thing that bothers me most is that the geometric distribution should be defined for constant probabilities. But at the same time, the math (or some aspects of it) logically make sense from a distance. I'll be boggling my head around this for awhile as I do other things. Can't guarantee as much usefulness as some other Joe Schmoe though.

Some thoughts that passed my mind:

1) It may be beneficial to write (or at least think of) your probability function (not probability mass function, ie. the "augmented geometric distribution") as a piecewise function that only accepts integer values of x from 1 to m. It's impossible to have the card when you've killed no enemies, and if you're guaranteed the card at m drops then the distribution is irrelevant after m as well.

Of course, this gives me headaches because questions arise about whether the final probability mass function is discrete or continuous, and whether it legitimately sums to 1 when using the appropriate summation or integration. But I'll leave that headache for another day.

2) Equation [23] (your "augmented geometric distribution" -- I'll be calling it this if you couldn't tell yet) breaks at x=1 because mathematical models cannot naturally adjust themselves to make practical sense. That is, the inclusion of sequential multiplication only makes practical sense when x > 1. If x = 1, then the number of trials is equal to 1, and P(X=1) = p1. No sequential multiplication is required, as denoted by equation [19]. If x > 1, then several failure terms (everything inside the sequential product) get multiplied all the way up to the instant where X = x. Thus, a less function-breaking representation would be a piecewise function equal to equation [19] when x = 1 and equation [23] when x > 1.

 

[Own]

I only skimmed this but I am against any system in an RPG based around optional collectables that makes those collectables drift towards an inevitability. I was being somewhat serious when suggesting, at most, a +1% after 1000 kills as something of a pity gesture.

It doesn't really bother me if someone doesn't manage to get all the cards and drops on their first playthrough. Few people do on their first run in an RPG. That's what NG+ or endgame grinding is for. I don't know of a single other RPG that uses an inevitability system.

I don't really have anything to add beyond that.

 

[XxX_MLG Noob_XxX]

I only skimmed this but I am against any system in an RPG based around optional collectables that makes those collectables drift towards an inevitability. I was being somewhat serious when suggesting, at most, a +1% after 1000 kills as something of a pity gesture.

It doesn't really bother me if someone doesn't manage to get all the cards and drops on their first playthrough. Few people do on their first run in an RPG. That's what NG+ or endgame grinding is for. I don't know of a single other RPG that uses an inevitability system.

I don't really have anything to add beyond that.

The first thing I wanna say is that cards cannot be considered "optional" as they are right now. A lot of people exist who want that feeling of "100%". This feeling is especially more likely to appear in SoG because 100% is more reasonable in SoG compared to...say...getting all achievements in TF2. If cards weren't required for full completion, it would feel different. For instance, I don't have everything in Terraria. But having all the achievements gives me a sense of "100% completion", so I'm satisfied not to go out and look for every item/buff/etc.

The problem is that the cards become much less relevant with end game grinding. A lot of previous enemies get 1-shot quite easily and grinding just becomes a very boring process. Sometimes it's just straight up annoying if you're at places like the toy factory or temple of seasons (tornado spam, etc.). Sure, you can grind to get 100%. But the motivation to do so is much smaller when the path before you is much more boring (and you have no idea if it'll take you 5 hours to get a card). As for NG+, it's really only worth while if the game is made sufficiently interesting in the second iteration. Otherwise, you're still in boring grinding.

I don't play many other games but I imagine the card mechanic is fairly uncommon. The problem it brings up is permanent buffs that are separate from stat-improvement obtained by crafting/finding special items from enemy drops... If cards didn't give buffs or 100%, no one would really care about them. But then, they would have no reason to exist. On the other hand, if cards give buffs and are required for 100%, things change significantly. It doesn't help that some people have legitimately spent ~10 hours on a single card. Those are the kinds of stories people want to avoid, and it's why a lot of people want a change in the drop rate in any given playthrough (not just an NG+). Even if you say "those situations are rare" or more accurately "probably rare" (neither of us have data), it isn't fair to shove any valued player into such a harsh time category.

It doesn't matter whether or not SoG follows the same patterns as other games when it comes to card drops (more specifically rng). SoG is not other RPG games, nor should it be bound by them. (Bound does not mean inspired.) And the devs can handle it however they please. It'll still be amazing game if the probability "drifts towards inevitability". The most important aspect of any game is that overall it's made an enjoyable experience for everyone. If it can't be enjoyable for everyone, then it should be enjoyable for most people with compromise for the few upset ones. If that can't be done, then it's simply made enjoyable for most people. If SoG is "supposed to be about grinding" (still doesn't justify making someone fight boring enemies for 10 hours), then the grinding itself should be enjoyable. If it's some mundane process, then everyone (*most people) will despise it.

Life would be easier if cards didn't exist because the debate wouldn't exist either. But since they're here now, the hole's too deep, and removing them or nullifying them wouldn't make sense. I don't necessarily think the cards should come super easily to anyone. I'll comment more about that in a separate reply later. But I do believe that the distribution should be changed such that the 10-hour-grinding-for-1-card people never ("never") exist. (I say "never" because stats.) It's awful to let that happen to players, even if it's just one of them. Everyone matters.

Instead of thinking inside fixed rules, I think it's more beneficial to think of the greater picture and how every player is affected and can possibly be affected. If a probability is 0.01% and drifts to 100% over the course of 900 trillion kills, it's not a big deal; people will pretty much always feel the nasty rng and never the blissful "near-guaranteed rng". The problem isn't the possibility of a drop being guaranteed as time goes on (or as more enemies are killed). The problem is the drop being given too early, or too late. And I think G has come up with something that can address that problem well.

I know you don't like long comments; so if you don't read this, that's fine. This was kind of a response to you but also a general comment for everyone to see. I'll post my feelings about where (or roughly where) the card drop probabilities should fall later.

 

[res7less]

I actually read the entire thing, well, except for the software how-to part and I understood probably about 70% of it. Which is probably a joke, since you oversimplified it anyway Oh, man, at what point did my russian math brain stop to function?

Anyways, first off, it's awesome how much effort you put into all that math and the graphs. That post could be already considered somewhat of a miniature thesis on loot systems in games.

Then, for the group I'm in, um... probably 5.3 or 5.4. But before I elaborate, I have a one definite and one potential comprehension question to make sure I get it.

1. The unit step method is not just adding a flat value to the drop rate per kill, right? Or, if it is, does it consider a drop rate cap?

2. When we talk about multiplayer, do the same rules still apply? Because in the starting explanation one of the conditions was that after a success, the trials end. But in multiplayer the trials don't end on the first success, but only when the last player gets the same type of card. Or is it easy to apply the same rules to multiplayer with some tweaks?

My overall opinion: I like an approach that tries to tackle a problem starting with its core, especially when it's done as thoroughly as you did (and even adding things for completeness' sake even though you didn't consider them necessary). But the way I see it, the core problem is trying to reduce the number of extremely unlucky players, right? Basically get the graph to get towards infinity faster (assuming we don't want a completely certain drop at some point).

So, if we are to incorporate a kill count into a formula anyway, what hinders us just adding a flat value of, let's say 0,03% to the drop rate per kill? Doesn't it serve the same purpose? And if we don't want a definite drop, we could cap the drop rate at let's say 10%. Yeah, you would still "potentially" get to infinity, but how likely is it to roll >10 fifty times in a row. And that's after the drop rate was maxed out, which still requires you to kill 333 monsters.

I'd take an elegant solution any day, but probably not at the price of adding unnecessary complexity (the unnecessary part is just my estimation, I might be completely wrong here). Because, I mean, the reason almost any loot system uses unweighted geometric distribution is because it's quick&dirty and 90% of the time it works every time. And because no one wants to shoot birds with a death star. But if we are to deviate from the norm (which I absolutely agree with) by making the connection between kills and drop rate anyway, there probably could be simpler ways.

Also, and that's another assumption based on my minor programming experience, don't long numbers create more room for inaccuracy due to rounding and thus, bugs? Just a thought that occurred when seeing the value of a in 4.4.

If, however, it's not as difficult to implement as I think it is, I withdraw and totally claim the contrary of what I said! Though I'd probably still use a flat increase with a probability cap if I would want to build a loot system.

PS: "Aftermath", haha <3

 

[XxX_MLG Noob_XxX]

Reading your article, reading Own's comments, seeing previous comments from everyone, thinking about card drops, and thinking about my own gameplay overall have made me change my philosophy of how cards should be given to people. Of course, I don't have a well-defined thesis or anything. I just have a general idea. What matters is that the idea is new and kind of tosses me into one of G's categories.

As a precursor, I kind of prefer G's 5.6, but only to the extent that players are less likely to get cards early. I have mixed feelings about players getting them much easier later on if the probability becomes extremely favorable in...say...10 kills for instance. (That's just an example, I don't know exactly how the maths play out.) A probability that increases gradually, but not absurdly, is what I desire. The bold statements will effectively give you a TL;DR version.

Here's a crazy thing that I realized. When I go back to fight some bloomos or rabbys or whatever else after the first boss...and I get that bloomo/rabby/bee card in the first 20-30 kills or less (if I do), I feel a rush of exhilaration! But recently I've had to ask myself...Why? Because I got a cool new buff? No. Because I'm that much closer to 100% completion? Hm...not that either. No. I get excited when I get cards insanely early because it means that's one less card that I have to worry about potentially spending 3-10 hours of my valuable time grinding for. At some point in your grinding, especially end-game, there comes a point where grinding for cards is literally a time sink. There is no benefit for it whatsoever: no level ups (at least not quickly), no amazing drops (assuming you already got them), no extra skill points or anything else. And that isn't to say that those things should necessarily be provided if you're taking forever to grind cards (though maybe slightly easier level ups would make it more worthwhile)...but that is to point out that eventually, card grinding effectively becomes a waste of time. (Yes, getting stat boosts and getting closer to 100% is nice and not a waste, but if an incredibly large amount of time is spent doing it then it's a lot of real-life time burned for no good reason.)

I'm sure I'm not the only person who feels that way when it comes to getting cards early. The one thing a lot of people dread when it comes to finishing another 100% save file is spending so many hours of their time grinding for cards (and possibly hating it). The problem is that cards shouldn't have that effect. The primary sense of exhilaration for getting a card drop should be a feeling of accomplishment for good hard work, not a sense of relief of not having to grind for the next 7 hours for a given card. (I say "primary" because I'm sure everyone feels some sense of accomplishment upon attaining a card. For some it may even primarily be accomplishment, even if it took 30,000 hours. That ain't me though. lol.)

So what am I getting at? The point is that I feel like card drops do not properly reflect a player's hard work. I conclude this from the response of getting a card early ( "that's one less thing I have to waste my life on" ), the dread of starting a new 100% story file ( "all the hours I have to spend grinding, never knowing when a card will drop ):" ) and the pains a person feels after not getting the card within 9 hours ("I've spent 9 hours on this! I deserve a card! ):<"). That is, due to probability, several situations exist where a person is given a card too early (not given a rewarding feeling, but a relieving one) and where a person is given a card too late (again, not given a rewarding feeling, but given frustration at not getting a card within a reasonable time frame). And I feel that neither situation gives a proper reward/sense of accomplishment to the player.

My proposition would be to make cards completely unobtainable until a certain number of kills are reached. Then, engage the probability distribution and adjust it so that the card drop is obtained "roughly around" where the desired kill-count-average for the enemies is. From a lore based stand point, it doesn't make any sense for a player to get a card from any enemy within 10 or so kills (no matter how lucky they are). I guarantee you that was not how Zhamla Meer got his cards. No. He used Super Deep Pass Thundaza Overdrive (lol) and killed groups of boars at once until he got the cards we he was after. (Because of that, he still gets cards easier than us. haha.) Of course, as I've previously said, we don't want people taking trillions of hours to get cards, so the distribution should still be kind to them. Ideally, the distribution would yield 0 below the minimum kill count, kick in after the minimum kill count, and gradually increase as G has described it such that the card drop occurs within a fair time frame. Of course, the minimum kills necessary for a given enemy could be adjusted if desired. (I wonder if that's necessary though. A global minimum may be more beneficial).

 

[XxX_MLG Noob_XxX]

1. The unit step method is not just adding a flat value to the drop rate per kill, right? Or, if it is, does it consider a drop rate cap?

What G calls "the unit step method" (I'd call it the degenerative distribution method but no one cares) does not have any "drop rates" per se. It just looks at the kill count...and if the kill count is below the proper amount, you never get a card. Once the kill count reaches the proper amount, you get a card (and there's no need to run the check anymore). You could basically get away with something vaguely similar to

...
update(rabbys_killed);
if (rabbys_killed == 300) {
rabby_card = 1;
// End card check loop here
}
...

So, if we are to incorporate a kill count into a formula anyway, what hinders us just adding a flat value of, let's say 0,03% to the drop rate per kill? Doesn't it serve the same purpose? And if we don't want a definite drop, we could cap the drop rate at let's say 10%. Yeah, you would still "potentially" get to infinity, but how likely is it to roll >10 fifty times in a row. And that's after the drop rate was maxed out, which still requires you to kill 333 monsters.

I only skimmed this but I am against any system in an RPG based around optional collectables that makes those collectables drift towards an inevitability.

I feel like scaling and exponentiation give much greater freedom to the designer because you can adjust how quickly things change. Flat rates are hard because you have to adjust them according to how much time you're wiling to force the player to grind while avoiding shooting the probability up too quickly for only a small amount of kills. The beauty of scaling and exponentiation is that you can start with gradual improvements and end with major improvements for someone who's very unlucky. There are other justifications as well. This doesn't necessarily prove it to be the best or most reasonable option, but it's definitely more free and robust.

I think your idea about capping at a particular value (eg. 10%) is spectacular. 10% is an example of a compromise between Own's (and a few others') distaste and what a majority of other people want. 10% is never guaranteed, but you shouldn't be grinding for too much longer at that point. Of course, it complicates the distribution, but what can you do? Sorry to ping you again Own, but I figured res7less' idea would be of some interest to you.

 

[MrChocodemon]

Put me in category 5.7 with Own

I think that this approach would be minorly shifting favors for really unlucky people, which might not stop complaints/rants, but stops possible, though unlikely, infinite farming sessions.

My approach would be:

• a hard number of kills that has to be reached befor a card can even drop.
• a low percentage for card drops
• and minor increase of drop chance per x kills

And those values can be adjusted per enemy.

While rabbies might be
- after 100
- base chance of 0,3%
- each 30 kills increase chance += 0,05%

And Peckos have
- after 20
- base chance of 0,1%
- each 10 kills increase chance += 0,01


Effects

• easy to implement
• easy to adjust
• no first kill drops
• no-infinite-grinding guarantee + lessend frustration
• lower performance impact than multiplicative math

 

[XxX_MLG Noob_XxX]

My approach would be:

• a hard number of kills that has to be reached befor a card can even drop.
• a low percentage for card drops
• and minor increase of drop chance per x kills

And those values can be adjusted per enemy.

While rabbies might be
- after 100
- base chance of 0,3%
- each 30 kills increase chance += 0,05%

And Peckos have
- after 20
- base chance of 0,1%
- each 10 kills increase chance += 0,01

I feel like it would be nicer to have a more friendly drop rate increase if a "no cards before X kills" idea is implemented. I'm all for no cards before X, and X can be the same across all enemies if desired (or not). But keeping a player from obtaining a card until X drops also increases grinding time and distorts the "global" distribution. For instance, by the time 300 rabbies are killed with your example (I know it's just an example), the probability of getting a rabby card is roughly double its original value. But that value is only 0.6% (below the value of say, an original elite), and it appears after the original mean 300 has been passed. Moreover, the player has wasted 100 potential rolls for getting a rabby card, 1/3 of the mean/expected value. So in a sense, it doesn't guarantee less frustration and can perhaps increase it for some.

I can get low base rates, and I love the idea of no cards before X. But why should the drop rate stay low for "virtually/perceptually" extremely small over "all time" ( < 1%).

 

[The G-Meister]

Thanks for the kind words guys, and moreover thanks for reading that monster of an article. I'm currently on a bit of a vacation in the Isle of Wight, and as such replies are likely to be slow, so thanks MLG for answering some of the questions already.

To @MrChocodemon and @Own, fair enough, I see where you're coming from. The reason I didn't approach from this angle is that I wanted to put the stats of the distribution first. This means putting complete control into the implementers hands, and as such, being able to directly control both the average drop point and the amount of spread the people have. Not only that, but have a direct and simple comparison to make between the card drops of different enemies. This distribution has those properties somewhere that are directly modifiable and comparable to the current system. When it comes to additive drop rates, I have no idea how to even begin analysing them for statistics.

Furthermore, I wanted it to be easy to implement, which is where I come with one of a couple replies to @res7less. Any distribution that doesn't come as a single formula will always have at least another section of code included. For example, increasing the drop rate every 10 kills requires an "if the number of kills over ten has a remainder of zero, add 0.01 to the drop rate". It may seem insignificant, but it's still a tiny extra bit of work the devs have to do. The implementation for this is legitimately what I said in the article, being add a kill counter and swap a constant for a formula. It also doesn't take half a second to boot up the computer tool and type in a couple number. The hack I suggested to Teddy is just an even more streamlined way of implementing it, by replacing the formula with a much easier to write method, and have the formula in a global place that can be accessed by all types of enemy.

On the topic of large decimals, Res7, It's actually quite the opposite. The more decimal points you have for a decimal value, the more accurate calculations involving that value will be. Of course there is an element of computer error and that is one reason why we don't need to be 100% mathematically rigorous. However, by maximising the number of figures that number has, the more accurate we get.

Finally, I'd like to give a way in which it is possible to implement this distribution using MLG's idea of "no cards before a certain number of kills". It's actually fairly simple. Let's call this number of kills n. All we need to do is swap m for m - n and k for k - n, and the corresponding scaling factor generated for those values. Finally, in the game code, only start taking values from the distribution when the kill count hits n. If I can, let's show you it in action.

The graph below has m as 100 and k as 50, my usual testing values. However, the different lines have different values of n, as shown in the key. The graphs are of the usual format, being p(x), P(X = x) and P(X <= x), in that order.



Excuse the probably less informative colours. Unfortunately the closer n gets to k, the more steep the increase in drop chance becomes. The only way to mitigate that would be to add an extra correction factor which requires trial and error within trial and error, which frankly I don't have the inclination to even try trying There, a proof of concept will have to do.

 

[Own]

a hard number of kills that has to be reached befor a card can even drop.

This ruins the chance for speedrunners to get a lucky card drop. A little RNG is good for a healthy speedrunning community around a game.

 

[XxX_MLG Noob_XxX]

a hard number of kills that has to be reached befor a card can even drop.

This ruins the chance for speedrunners to get a lucky card drop.

But you're speaking for a small group of people on a topic that isn't significant. The idea of cards and permanent buffs -- from both a game and lore standpoint -- is not to luckily get one after killing an enemy or two. Speed runners will be able to do just fine without lucky card drops, and it even improves the overall challenge of a run. In fact, it would make things more fair/balanced for speedrunners overall because it would remove an element of unfair rng when comparing time "scores". Speedrunners being unable to get lucky card drops has no negative impact on the positivity of requiring a fixed number of kills before allowing cards to drop; as I said, it's actually beneficial for the speedrunning community.

What is important is a reevaluation of what cards are there for. We have to look at the way the player should be rewarded, the connection to the lore, the overall player experience, etc. etc. A game where people have to grind for centuries to get a card and a game where people can get a card in 10 kills are both poorly designed. (see the long comment I made earlier.)

 

[MrChocodemon]

This ruins the chance for speedrunners to get a lucky card drop. A little RNG is good for a healthy speedrunning community around a game.

A little yes, but having to kill a small base of enemies ruins only things, if you never kill more than the base amount. (Obviously, but it leads into my question)

Can you even beat Zhamla without grinding at all? Would that really affect speedrunners, or would it mean that they need to focus their grinding better.

Would it hinder speedrunning, or would it open a little more tactics and route planning, while also increasing droprates, which basically would make speedrunning grindsession a tiny bit more reliable.

Aren't speedruns which receive best times based on pure luck kind of bad for the SR community?

I have no idea about the SR community and am generally curious, if Gs appraoch would be better for SR. That would be definitly something to consider.

ALSO THIS

A game where people have to grind for centuries to get a card and a game where people can get a card in 10 kills are both poorly designed.

 

[The G-Meister]

I won't take an opinion on what "better" means for speedrunners, but the way the weighting works for this distribution is by making the less lucky people more lucky, and the more lucky people less lucky, to a point where everyone has a more consistent "luck". Look at the cumulative distribution graphs in 4.2.6. B for reference - there is less area under the graph before the mean, with the consequence of also less area over the graph after the mean. As a consequence it is less likely for them to get a drop no matter which weighting option is used, though still possible, and more probable than MLG's approach. However as I showed ealier, the distribution can be adapted to make MLG's idea work.

 

[Own]

A game where people have to grind for centuries to get a card and a game where people can get a card in 10 kills are both poorly designed.

Which, in my opinion, is a ridiculous stance to have considering every other RPG in history works this way. Including the Castlevania GBA / DS games, which featured a system identical to SoG's cards. Except they were called Souls and every enemy had one.

Trying to rig the 'luck' behind the scenes to try and ensure the majority of players gets something at around the same time removes the concept of a rare drop and turns it more into a kill quest with a bit of wiggle room masquerading as luck. You're unnaturally unlikely to get it on your first kill, or first ten, but at kill 50 you have a so-so chance and kill 100 you've got a great chance. Which is a system that only really works in any satisfying way if the player has no idea it actually exists. If they know that the game is secretly fudgeting the numbers the idea and thrill of anything being a rare find vanishes.

I'm 100% in opposition to making drops less likely to happen early on just to ensure that a majority gets them at a specific grind amount. The only time RNG should be adjusted favorably or unfavorably (outside things the player can use to manipulate them) is when a threshold has been breached that's genuinely unfair to players time. I'm not sure what exactly that threshold is - 250 kills? 500? 1000? - but you don't need to completely overhaul the system from beginning to end when the only problem exists at the far end for an incredibly small percentage of outliers.

 

[MrChocodemon]

I won't take an opinion on what "better" means for speedrunners,

fair enough